数学常用知识总结

一些常用的数学知识。

前导知识

这个前导知识并不关于数学知识，仅是为了总结$\LaTeX$中导数、积分的表示方法。

1. 偏导符号

   $ \frac{\partial f}{\partial x} $  # 一阶
   $ \frac{\partial ^{n} f}{\partial x^{n}} $  # n阶

   效果：$ \frac{\partial f}{\partial x} $和$ \frac{\partial ^{n} f}{\partial x^{n}} $

2. 求导符号

   $ \frac{\mathrm{d} y }{\mathrm{d} x} $  # 一阶
   $ \frac{\mathrm{d}^{n} y }{\mathrm{d} x^{n}} $  # n阶

   效果：$ \frac{\mathrm{d} y }{\mathrm{d} x} $和$ \frac{\mathrm{d}^{n} y }{\mathrm{d} x^{n}} $

3. 撇形式的求导符号

   $ \frac{ y' }{ x' } $

   效果：$ \frac{ y’ }{ x’ } $

4. 单个积分符号

   $ \int_{X}^{Y} \exp(z)\, dz $

   效果：$\int_{X}^{Y} \exp(z)\, dz$

5. 多重积分符号

   $ \iiint_{-X}^{Y} \exp(z)\, dz $	# 三重积分，需要几重就往前面加几个i

   效果：$ \iiint_{-X}^{Y} \exp(z)\, dz $

6. 曲线积分符号

   $ \oint_{C} o^2+p^2 do\,dp $

   效果：$ \oint_{C} o^2+p^2 do\,dp $

7. 极限符号

   $ \lim_{n\to\infty} $

   效果：$\lim_{n\to\infty}$

8. 目前所需只想到这些，如后续有需要，再做进一步的补充。

函数的奇偶性

设$f(x)$是定义在$[-l,l]$上的任意函数，则

$$F_1(x)=f(x)-f(-x)必为奇函数；F_2(x)=f(x)+f(-x)必为偶函数。$$

1. 奇函数$y=f(x)$的图形关于坐标原点对称，当$f(x)$在$x=0$处有定义时，必有$f(0)=0$。

2. 偶函数$y=f(x)$的图形关于y轴对称，且当$f’(0)$存在时，必有$f’(0)=0$。

3. 函数$y=f(x)$与$y=-f(x)$的图形关于$x轴$对称；函数$y=f(x)$与$y=f(-x)$的图形关于$y轴$对称；函数$y=f(x)$与$y=-f(-x)$关于原点对称。

4. 函数$y=f(x)$的图形关于$x=T$对称的充分必要条件时

   $$f(x)=f(2T-x)或f(x+T)=f(x-T)$$

关于函数性质的重要结论

关于$f’(x)和\int_a^x f(t)dt$的性质才是这个知识的落脚点。

1. 若$f(x)$是可导的偶函数，则$f’(x)$是奇函数。
2. 若$f(x)$是可导的奇函数，则$f’(x)$是偶函数。
3. 若$f(x)$是可导的周期为$\ T \ $的周期函数，则$f’(x)$也是以$ \ T \ $为周期的周期函数。
4. 连续的奇函数的一切原函数都是偶函数。
5. 连续的偶函数的原函数中仅有一个原函数是奇函数。
6. 若连续函数$f(x)$以$\ T \ $为周期且$\int_0^T f(x)dx=0$，则$f(x)$的一切原函数也以$\ T \ $为周期。
7. 若$f(x)$在有限区间$(a,b)$内可导且$f’(x)$有界，则$f(x)$在$(a,b)$内有界。

重要的函数

心形线（又称外摆线）

表达式为$r=a(1-cos\theta) \ (a>0)$

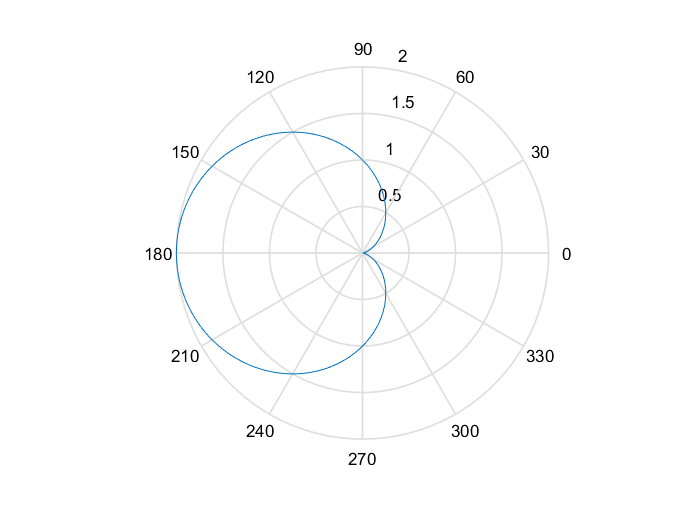
这个表达式的右端是以$2\pi$为周期的周期函数，作图时只要考虑$0 \le \theta \le 2\pi $就可以，并且，对于方程的右侧，$\theta$换做$(2\pi-\theta)$时，其值不变，也就是说心形线以极轴为对称轴。

玫瑰线

三叶玫瑰线表达式为：$r=asin\ 3\theta \ (a>0)$

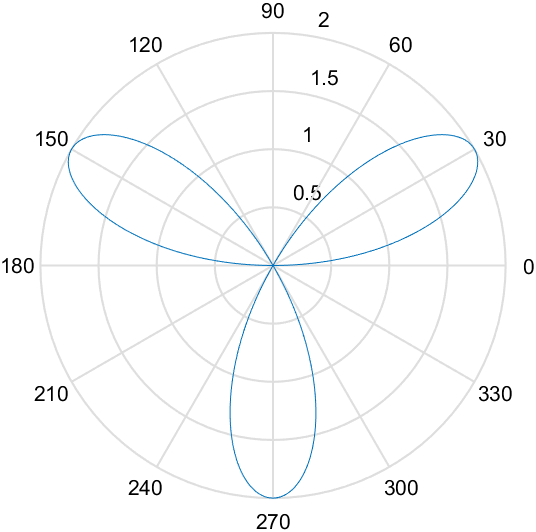
这个表达式右端是以$\frac{2\pi}{3}$为周期的周期函数。

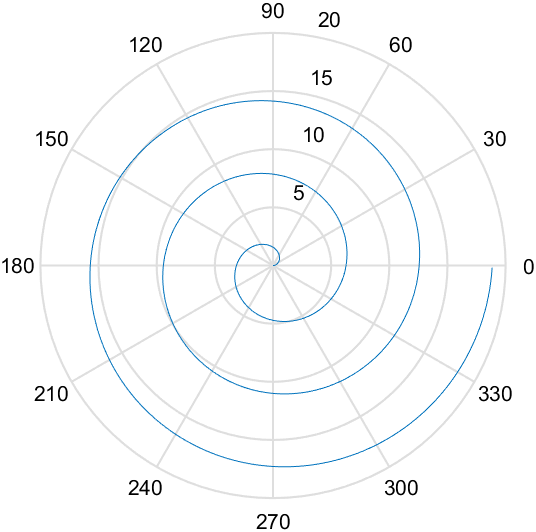
阿基米德螺线

阿基米德螺线的表达式为：$r=a\theta \ (a>0,\theta \ge 0)$的图形。

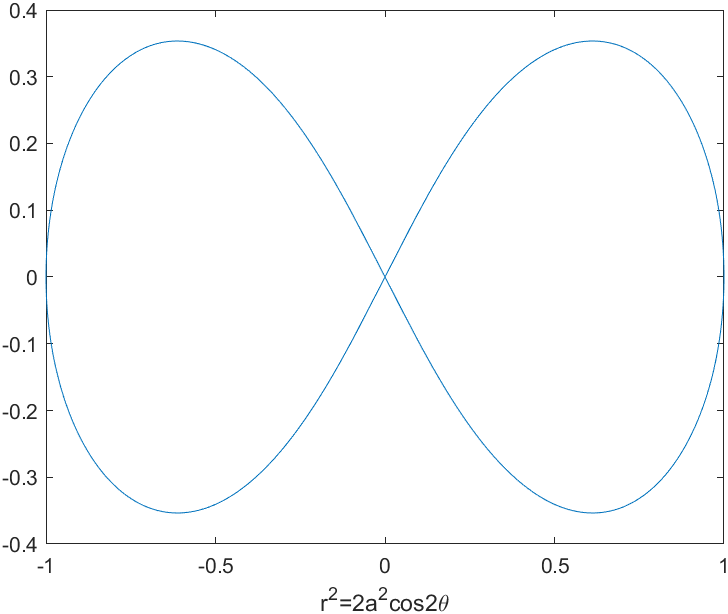
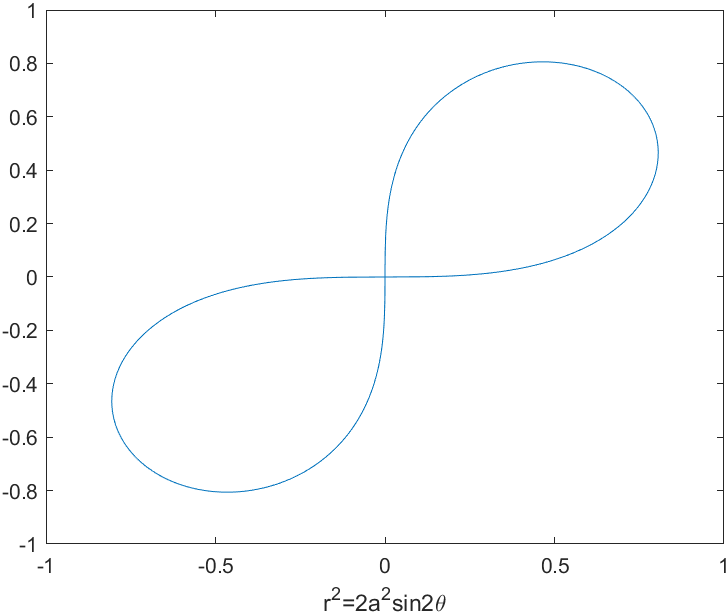
伯努利双纽线

设定线段$AB$长度为$2a$，动点M满足$MA \ \cdot \ MB=a^2$，那么$M$的轨迹成为双纽线。

取$AB$为$x$轴，中点为原点，那么$A,B$的坐标分别为$(-a,0),(a,0)$。设$M(x,y)$，则有

$$\sqrt{(x+a)^2+y^2} \ \cdot \ \sqrt{(x-a)^2+y^2}=a^2,$$

整理得$(x^2+y^2)^2=2a^2(x^2-y^2)$.

在极坐标中，可化简得$r^2=2a^2cos \, 2\theta$.

摆线

摆线的参数方程为：

$$\begin{cases} x=r(t-sin\,t), \\ y=r(1-cos\,t). \\ \end{cases}$$

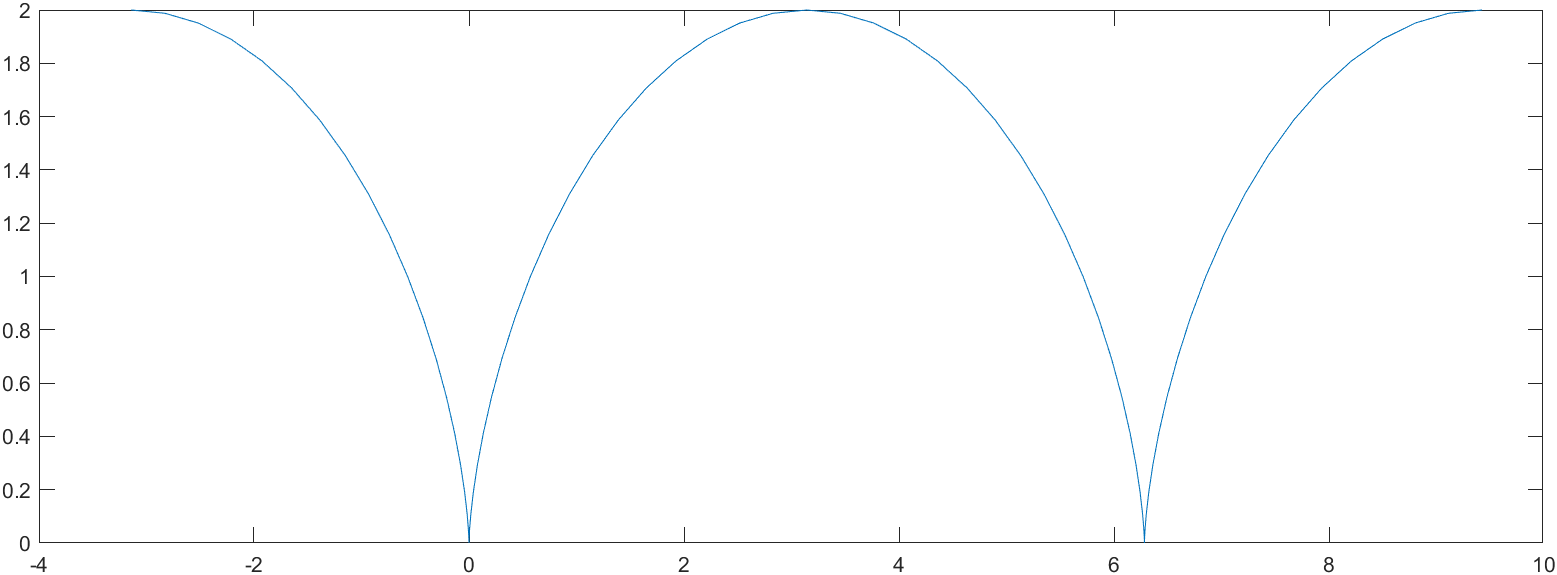
摆线具有周期性，周期$T=2\pi$，由图我们可以知道第一个拱的拱顶的坐标为$(\pi r,2r)$.

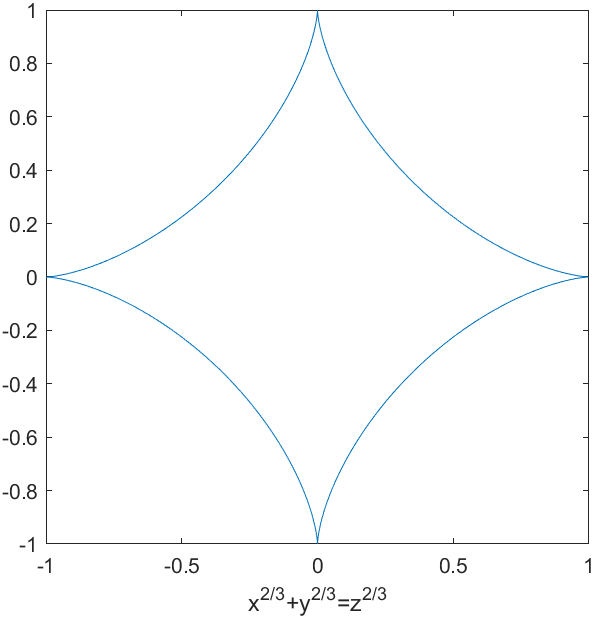
星形线

星形线的参数方程为：

$$\begin{cases} x=rcos^3t, \\ y=rsin^3t. \\ \end{cases}$$

若消去$t$，可得$x^\frac{2}{3}+y^\frac{2}{3}=z^\frac{2}{3}$，此为直角坐标方程。

数列

等差数列

首项为$a_1$，公差为$d \ (d\ne0)$的数列$a_1,a_1+d,a_1+2d,\cdots,a_1+(n-1)d,\cdots$.

1. 通项公式$a_n=a_1+(n-1)d$
2. 前$\ n \ $项的和$S_n=\frac{n}{2} \left[2a_1+(n-1)d\right]=\frac{n}{2}(a_1+a_n)$.

等比数列

首项为$a_1$，公比为$r \ (r\ne0)$的数列$a_1,a_1r,a_1r^2,\cdots,a_1r^{n-1},\cdots$.

1. 通项公式$a_n=a_1r^{n-1}$

2. 前$\ n \ $项的和：

   $$S_n= \begin{cases} na_1, \qquad \quad r=1, \\ \frac{a_1(1-r^n)}{1-r}, \quad \ \ r \ne 1. \end{cases}$$

3. 常用$1+r+r^2+\cdots+r^{n-1}=\frac{1-r^n}{1-r} \quad (r\ne 1).$

4. 一些常用数列前$\ n \ $项的和：

   $$\sum_{k=1}^n k=1+2+3+\cdots+n=\frac{n(n+1)}2. \\ \sum_{k=1}^n k^2=1^2+2^2+3^2+\cdots+n^2=\frac{n(n+1){n+2}}6. \\ \sum_{k=1}^n \frac{1}{k(k+1)} = \frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \cdots + \frac{1}{n(n+1)} = \frac{n}{n+1}.$$

三角函数

基本关系

$$csc \ \alpha = \frac{1}{sin \ \alpha}, \ sec \ \alpha = \frac{1}{cos \ \alpha}, \ cot \ \alpha = \frac{1}{tan \ \alpha}, \\ \\ tan \ \alpha = \frac{sin \ \alpha}{cos \ \alpha}, \ cot \ \alpha = \frac{cos \ \alpha}{sin \ \alpha}, \\ \\ sin^2\alpha+cos^2\alpha=1, \ 1+tan^2\alpha=sec^2\alpha, \ 1+cot^2\alpha=csc^2\alpha.$$

诱导公式

$$sin(\frac\pi2-\alpha)=cos\ \alpha, \quad sin(\frac\pi2+\alpha)=cos\ \alpha, \\ sin(\pi-\alpha)=sin\ \alpha, \quad sin(\pi+\alpha)=-sin\ \alpha, \\ cos(\frac\pi2-\alpha)=sin\ \alpha. \quad cos(\frac\pi2+\alpha)=-sin\ \alpha, \\ cos(\pi-\alpha)=-cos \ \alpha, \quad cos(\pi+\alpha)=-cos \ \alpha, \\ tan(\frac\pi2-\alpha)=cot \ \alpha, \quad tan(\frac\pi2+\alpha)=-cot \ \alpha, \\ tan(\pi-\alpha)=-tan \ \alpha, \quad tan(\pi+\alpha)=tan \ \alpha, \\ cot(\frac\pi2-\alpha)=tan \ \alpha, \quad cot(\frac\pi2+\alpha)=-tan \ \alpha, \\ cot(\pi-\alpha)=-cot\ \alpha, \quad cot(\pi+\alpha)=cot\ \alpha. \\$$

倍角公式

$$sin \ 2\alpha=2sin\,\alpha cos\,\alpha, \\ cos \ 2\alpha=cos^2\alpha-sin^2\alpha=1-2sin^2\alpha =2cos^2\alpha-1,\\ sin \ 3\alpha=-4sin^3\alpha+3sin\,\alpha, \quad cos \ 3\alpha=4cos^3\alpha-3cos\,\alpha, \\ tan \ 2\alpha=\frac{2tan\,\alpha}{1-tan^2\alpha}, \quad cot \ 2\alpha=\frac{cot^2\alpha-1}{2cot\,\alpha}.$$

半角公式

$$sin^2\frac\alpha2=\frac12(1-cos\,\alpha), \quad cos^2\frac\alpha2=\frac12(1+cos\,\alpha), \ (降幂公式) \\ sin\frac\alpha2=\pm\sqrt\frac{1-cos\,\alpha}2, \quad cos\frac\alpha2=\pm\sqrt\frac{1+cos\,\alpha}2, \\ tan\frac\alpha2=\frac{1-cos\,\alpha}{sin\,\alpha} = \frac{sin\,\alpha}{1+cos\,\alpha} = \pm\sqrt\frac{1-cos\,\alpha}{1+cos\,\alpha},\\ cot\frac\alpha2=\frac{sin\,\alpha}{1-cos\,\alpha} = \frac{1+cos\,\alpha}{sin\,\alpha} = \pm\sqrt\frac{1+cos\,\alpha}{1-cos\,\alpha},\\$$

和差公式

$$sin(\alpha\pm\beta)=sin\,\alpha cos\,\beta \pm cos\,\alpha sin\,\beta,\\ cos(\alpha\pm\beta)=cos\,\alpha cos\,\beta \mp sin\,\alpha cos\,\beta,\\ tan(\alpha\pm\beta)=\frac{tan\,\alpha\pm tan\,\beta}{1\mp tan\,\alpha tan\,\beta},\\ cot(\alpha\pm\beta)=\frac{cot\,\alpha cot\,\beta \mp 1}{cot\,\beta\pm cot\,\beta}.\\$$

积化和差公式

$$sin\,\alpha cos\,\beta=\frac12\left[sin(\alpha+\beta)+sin(\alpha-\beta)\right],\\ cos\,\alpha sin\,\beta=\frac12\left[sin(\alpha+\beta)-sin(\alpha-\beta)\right],\\ cos\,\alpha cos\,\beta=\frac12\left[cos(\alpha+\beta)+cos(\alpha-\beta)\right],\\ sin\,\alpha sin\,\beta=\frac12\left[cos(\alpha-\beta)-cos(\alpha-\beta)\right].\\$$

和差化积公式

$$sin\,\alpha+sin\,\beta=2sin\frac{\alpha+\beta}2cos\frac{\alpha-\beta}2,\\ sin\,\alpha-sin\,\beta=2sin\frac{\alpha-\beta}2cos\frac{\alpha+\beta}2,\\ cos\,\alpha+cos\,\beta=2cos\frac{\alpha+\beta}2cos\frac{\alpha-\beta}2,\\ cos\,\alpha-cos\beta=-2sin\frac{\alpha+\beta}2sin\frac{\alpha-\beta}2.\\$$

万能公式

若$u=tan\frac{x}2(-\pi<x<\pi)$，则

$$sin\,x=\frac{2u}{1+u^2},\ cos\,x=\frac{1-u^2}{1+u^2}.$$

因式分解

1. $(a+b)^2=a^2+2ab+b^2$

2. $(a-b)^2=a^2-2ab+b^2$

3. $(a+b)^3=a^3+3a^2b+3ab^2+b^3$

4. $(a-b)^3=a^3-3a^2b+3ab^2-b^3$

5. $a^2-b^2=(a+b)(a-b)$

6. $a^3-b^3=(a-b)(a^2+ab+b^2)$

7. $a^3+b^3=(a+b)(a^2-ab+b^2)$

8. $a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+\cdots+ab^{n-2}+b^{n-1})(n是正整数)$

9. $n\ $是正偶数时，$a^n-b^n=(a+b)(a^{n-1}-a^{n-2}b+\cdots+ab^{n-2}-b^{n-1})$

10. $n\ $是正奇数时，$a^n+b^n=(a+b)(a^{n-1}-a^{n-2}b+\cdots-ab^{n-2}+b^{n-1})$

11. 二项式定理

    $$(a+b)^n=\sum_{k=0}^nC_{n}^ka^{n-k}b^k=a^n+na^{n-1}b+ \frac{n(n-1)}{2!}a^{n-2}b^2 +\cdots+ \\ \frac{n(n-1)\cdots(n-k+1)}{k!}a^{n-k}b^k+\cdots+nab^{n-1}+b^n.$$

常用不等式

1. 设$\ a,b\ $为实数，则$① \left| a\pm b \right|\le\left|a\right|+\left|b\right|;②\big|\left|a\right|-\left|b\right|\big|\le\left|a-b\right|$

   1. 离散情况下：设$ \ a_1,a_2,\cdots,a_n \ $为实数，则

      $$\left|a_1\pm a_2\pm\cdots\pm a_n\right|\le\left|a_1\right|+ \left|a_2\right|+\cdots+\left|a_n\right|.$$

   2. 连续情况下：设$\ f(x) \ $在$[\,a,b\,](a<b)$上可积，则

      $$\left|\int_a^bf(x)dx\right|\le \int_a^b \left|f(x)\right|dx$$
2. 1. $\sqrt{ab}\le\frac{a+b}2\le\sqrt{\frac{a^2+b^2}2}(a,b>0)$
   2. $\sqrt[3]{abc}\le\frac{a+b+c}3\le\sqrt{\frac{a^2+b^2+c^2}3}(a,b,c>0)$

3. 设$\ a>b>0 \ $，则$\begin{cases}
   当n>0时，a^n>b^n,\
   当n<0时，a^n<b^n,\
   \end{cases}$

4. 若$0<a<x<b,0<c<y<d,$则$\frac{c}b<\frac{y}x<\frac{d}a$.

5. $sin\,x<x<tan\,x\,(0<x<\frac\pi2)$

6. $sin \, x < x \ ( x > 0 )$

7. $arctan\,x\le x\le arcsin\,x\ (0\le x\le 1)$

8. $e^x\ge x+1 \ (\forall x)$

9. $x-1\ge ln\,x \ (x>0)$

10. $\frac{1}{1+x} < ln(1+\frac{1}{x})<\frac{1}{x} \ (x>0)$